Stående bølger på en streng

I dette eksperiment skal I undersøge resonansfænomenet på strenge af forskellig masse og som belastes forskelligt. God fornøjelse.
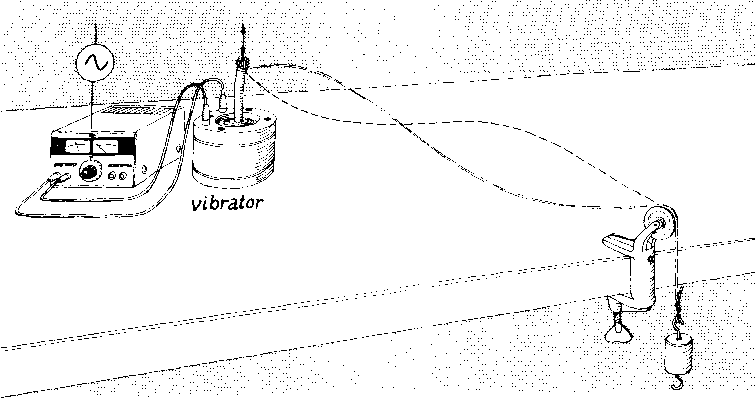
Principskitse af opstilling til måling af resonansfrekvenser
Måleproceduren kan være:
Procedure 1
- En passende snorlængde vælges f.eks. l = 1 m
- En streng opspændes med kendt masse, m / g
- Der belastes med 50 g (afhængig af strengens tykkelse)
- Der skrues op for frekvensen indtil, der er en flot resonansbue. Frekvensen aflæses og noteres.
- Belastningen øges med 50 g, punkt 4 gentages
- Punkt 5 gentages indtil der er foretaget 6 - 8 målinger.
- En anden streng vælges og ovenstående procedures punkt 2 - 6 gentages
- Punkt 7 gentages for de strenge, der er til rådighed.
Procedure 2
- En streng med diameter d = 0,50 og længde l på ca. 2m vælges.
- Der vælges en fast belastning på 100 g
- Strengen opspændes så den vandrette del bliver så lang som muligt. Længden måles (afpasses eventuelt til pænt tal ).
- Resonansfrekvensen for 1 bue bestemmes som ovenfor. frekvens og strenglængde noteres i skema 2.1
- Den vandrette del af strengen gøres kortere ved at flytte resonator nærmere til trissen. - ca. 20 cm. Ny længde måles og punkt 4 gentages.
- Punkt 5 gentages indtil lodderne ikke kan hænge frit over gulv mere.
Behandling:
Hvad kan I nu bruge disse data til? Det skulle helst fremgå at frekvensen ændrer sig, når I ændrer på de forskellige parametre - belastning, trådmasse og tråd længde. Så hvorfor ikke give jer til at undersøge følgende funktionelle sammenhænge?
- f : frekvens
- m: masse af svingende tråd
- ml: masse af belastningslodder
- l: længde af den svingende tråd. 2l = l.
- f(m): l holdes konstant, m varieres ved at benytte forskellige tråde. ml holdes konstant
- f(ml): l holdes konstant, m holdes konstant.
- f(l): m og ml holdes konstant
Undersøgelserne af sammenhængene sker bedst ved at afbilde datapunkterne i dobbeltlogaritmisk papir (eller ved at afbilde log(f) som funktion af log(parameter) i almindeligt millimeterpapir (herved får i bedre styr over akseindelingerne).
I konklusionen skal I så beskrive/kommentere de sammenhænge I mener I finder, der er mellem disse størrelser.
|
